4 Lab: Logistic Regression, LDA, QDA, and KNN

This is a modified version of the Lab: Logistic Regression, LDA, QDA, and KNN section of chapter 4 from Introduction to Statistical Learning with Application in R. This version uses tidyverse techniques and methods that will allow for scalability and a more efficient data analytic pipeline.

We will need the packages listed below. Order matters! We strategically load tidyverse after MASS so that the package dplyr from the tidyverse is loaded second. We do this because both packages have a select() function, and R will attempt to use the most recently loaded version of a function. This is called masking and you’ll get these warnings when you load packages with such conflicts. We can use dplyr::select() or MASS::select() to force R to use the function version from their respective package. This is cumbersome, so by loading dplyr second we are able to avoid having to use dplyr:select().

# Load packages
library(MASS)
library(tidyverse)
library(modelr)
library(janitor)
library(skimr)
library(broom)
library(corrplot)
library(class)

4.1 Data Setup

We have been discussing the concept and importance of training and testing data over the last few weeks. We will start to use it in practice now by using what is sometimes called a hold-out dataset, which is really just a test dataset. Before we implement this process let’s introduce the data we will be using for this lab.

We will be using the Smarket dataset from the ISLR library. Take a moment and inspect the codebook — ?ISLR::Smarket. This data set consists of percentage returns for the S&P 500 stock index over 1,250 days, from the beginning of 2001 until the end of 2005. For each date, we have recorded the percentage returns for each of the five previous trading days, Lag1 through Lag5. We have also recorded Volume (the number of shares traded on the previous day, in billions), Today (the percentage return on the date in question) and Direction (whether the market was Up or Down on this date).

In order to continue practicing the implementation of a coding structure that allows us to both scale and easily modify our workflow we will load this data from the provided Smaket.csv file. Notice that we re-type all character variables as factors.

smarket_dat <- read_csv("data/Smarket.csv") %>% 
  clean_names() %>% 
  mutate_if(is_character, factor)

We would typically proceed onto examining the data with numerical summaries and visualizations, but since we plan on creating a hold-out/test dataset we should do that first. We do not want aspects of the testing data to influence our modeling training/building process. There is a balancing act here because we first need to adequately process the data in order to ensure that both the training and testing datasets have the same data structure (e.g, variable types). Or we need to ensure that any data cleaning/processing pipeline we build for the training data can also be applied to the training data.

smarket_dat is fairly simple so we can proceed directly to splitting our data into testing and training. Since this is time dependent data we will use data pre-2005 (2001-2004) for training and the 2005 data for testing. We will store these in a tibble

data_db <- tibble(train = list(smarket_dat %>% filter(year < 2005)),
                  test  = list(smarket_dat %>% setdiff(train)))

Now let’s examine the training potion of our data.

data_db %>% 
  unnest(train) %>% 
  skim_without_charts()

TABLE 4.1: Data summary

Name	Piped data
Number of rows	998
Number of columns	10
_______________________
Column type frequency:
factor	1
list	1
numeric	8
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
direction	0	1	FALSE	2	Up: 507, Dow: 491

Variable type: list

skim_variable	n_missing	complete_rate	n_unique	min_length	max_length
test	0	1	1	9	9

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100
year	1	2002.52	1.11	2001.00	2002.00	2003.00	2004.00	2004.00
lag1	1	0.00	1.23	-4.92	-0.71	0.02	0.66	5.73
lag2	1	0.00	1.23	-4.92	-0.71	0.02	0.66	5.73
lag3	1	0.00	1.23	-4.92	-0.71	0.02	0.66	5.73
lag4	1	0.00	1.23	-4.92	-0.71	0.02	0.66	5.73
lag5	1	0.00	1.24	-4.92	-0.71	0.02	0.66	5.73
volume	1	1.37	0.27	0.36	1.21	1.37	1.51	2.78
today	1	0.00	1.23	-4.92	-0.71	0.02	0.66	5.73

# Proportions of Up/Down days
data_db %>% 
  unnest(train) %>% 
  count(direction) %>% 
  mutate(prop = n/sum(n))

## # A tibble: 2 x 3
##   direction     n  prop
##   <fct>     <int> <dbl>
## 1 Down        491 0.492
## 2 Up          507 0.508

# Correlations
data_db %>% 
  unnest(train) %>% 
  select(-direction, -test) %>% 
  cor() %>% 
  corrplot()

# Time trend in volume
data_db %>% 
  unnest(train) %>%
  ggplot(aes(x = seq_along(volume), y = volume)) +
    geom_line(alpha = 0.3) +
    geom_smooth(se = FALSE)

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'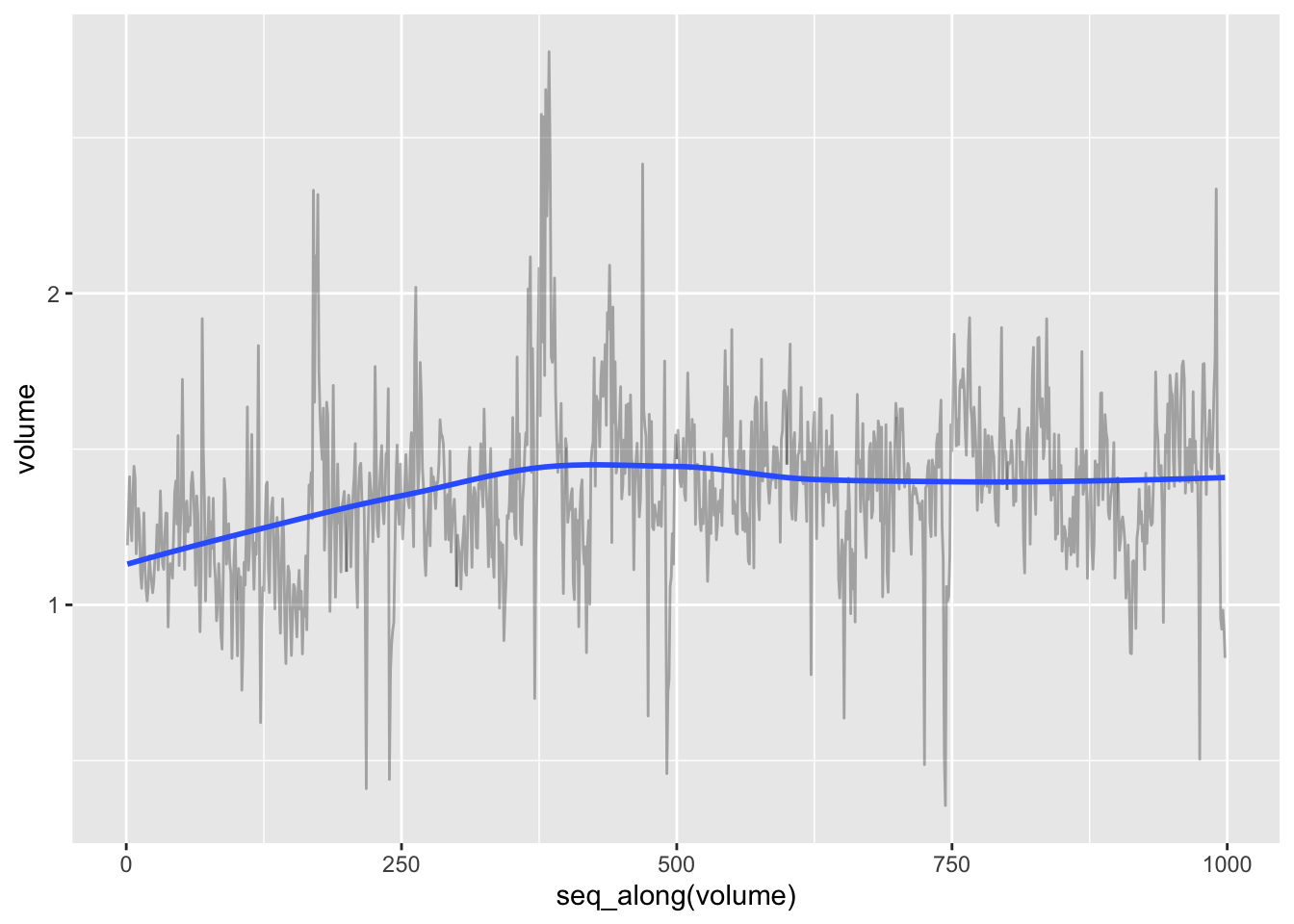

# Checking time trend for other variables
data_db %>%
  unnest(train) %>%
  select(-test) %>% 
  gather(key = variable, value = value, -year, -direction) %>%
  ggplot(aes(x = seq_along(value), y = value)) +
    geom_line(alpha = 0.3) +
    geom_smooth(se = FALSE) +
    theme(axis.text  = element_blank(),
          axis.ticks = element_blank()) +
    facet_wrap(. ~ variable, scales = "free")

FALSE `geom_smooth()` using method = 'loess' and formula 'y ~ x'

4.2 Logistic Regression

We will fit a few logistic regressions to attempt to predict whether the stock market will go down or up. Our set of possible predictors are the five lag measurements (lag1, …, lag5) and volume of volume of shares (in billions) traded on the previous day. We will train the models on the training dataset and then use the testing data set to validate and compare the models.

We will begin by only fitting a logistic model that uses all available predictors, but set up our workflow to allow us to easily include alternatively specified logistic models.

Let’s fit the model.

glm_fits <- data_db %>% 
  mutate(mod_01 = map(train, glm, 
                      formula = direction ~ lag1 + lag2 + lag3 + lag4 + lag5 + volume,
                      family = binomial))

Just like with linear models we can use tidy(), confint_tidy(), glance(), augment() and predict() to inspect the model. While we could store this information in glm_fits we will hold off on this for now because we first need to understand what we will be storing and why we want it stored. Secondly it would throw a wrench into our general workflow for fitting several models (look back on how we fit several linear models).

Let’s inspect the parameter estimates.

glm_fits %>% 
  pluck("mod_01", 1) %>% 
  tidy()

## # A tibble: 7 x 5
##   term        estimate std.error statistic p.value
##   <chr>          <dbl>     <dbl>     <dbl>   <dbl>
## 1 (Intercept)  0.191      0.334     0.573    0.567
## 2 lag1        -0.0542     0.0518   -1.05     0.295
## 3 lag2        -0.0458     0.0518   -0.884    0.377
## 4 lag3         0.00720    0.0516    0.139    0.889
## 5 lag4         0.00644    0.0517    0.125    0.901
## 6 lag5        -0.00422    0.0511   -0.0826   0.934
## 7 volume      -0.116      0.240    -0.485    0.628

Nothing, not even the intercept, is significant in this model. Indicating that there is no statistical evidence of an association between any of these predictors and direction. While none of the associations were significant, we are probably more interested in how well the model predicted direction. We can extract the predicted values using augment(), the .fitted values, or predict(). However augment() includes additional measures for model diagnostics (e.g. .hat, .cooksd, etc.) which can be useful. We will opt to use predict() for now since we want to focus on assessing the predictive capabilities of our model. We can and should circle back to model diagnostics for a more comprehensive understanding of our fitted model.

It is extremely important to understand what predict() returns for a logistic regression. Recall that we ultimately want a predicted direction (Up or Down). First note that without a newdata argument predict() returns a model’s predicted values for the data it was fitted/trained on. Next, let’s apply and actually inspect the values that predict() returns

glm_fits %>% 
  pluck("mod_01", 1) %>% 
  predict() %>% 
  skim_without_charts()

TABLE 4.2: Data summary

Name	Piped data
Number of rows	998
Number of columns	1
_______________________
Column type frequency:
numeric	1
________________________
Group variables	None

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100
data	0	1	0.03	0.09	-0.4	-0.02	0.04	0.09	0.4

We see predict() returns a numeric value and some of the values are negative and some are positive. Since we use logistic regression to predict the probability of a specified category (either Up or Down in this case), we should be concerned with negative values (probabilities cannot be negative). We need to realize that predict() is providing our predicted values on an alternative scale — log-odds for a binomial link. This is easy to remedy by setting type = "response", but it is easy to forget so take care with this — it also must be specified when using augment(). Now let’s inspect the predicted probabilities for the training data.

glm_fits %>% 
  pluck("mod_01", 1) %>% 
  predict(type = "response") %>% 
  skim_without_charts()

TABLE 4.3: Data summary

Name	Piped data
Number of rows	998
Number of columns	1
_______________________
Column type frequency:
numeric	1
________________________
Group variables	None

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100
data	0	1	0.51	0.02	0.4	0.49	0.51	0.52	0.6

We now have predicted probabilities ranging from about 0.4 to 0.6. What are these probabilities for though? We know they are for a direction, but are they the probabilities for Up or Down? This has to do with how the direction factor is encoded because predict(type = "response") returns the probability for the category that is designated to be 1 or in mathematical notation \(Pr(Y_i=1|X_i)\). Let’s check how direction was encoded when we loaded, processed, and assigned the data to smarket_dat.

smarket_dat %>% 
  # pull(): extract a column from a tibble - replacement for $
  pull(direction) %>% 
  contrasts()

##      Up
## Down  0
## Up    1

Since Up is assigned 1 we now know that the predicted probabilities are for Up. This is important because we can now change the predicted probabilities to predicted directions of the stock market. For observations with a predicted probability greater than 0.5 then we will assign it to Up, otherwise they will be assigned Down.

We will use demo_tib to demonstrate how to calculate and inspect predictions. This is to avoid altering glm_fits which will house several fitted logistic models and their associated information.

demo_tib <- glm_fits %>%
  mutate(train_prob = map(mod_01, predict, type = "response"),
         train_direction = map(train_prob, ~ if_else(.x > 0.5, "Up", "Down")))

# Predictions for train dataset
demo_tib %>% 
  unnest(cols = c(train, train_direction)) %>% 
  count(train_direction) %>% 
  mutate(prop = n / sum(n))

## # A tibble: 2 x 3
##   train_direction     n  prop
##   <chr>           <int> <dbl>
## 1 Down              331 0.332
## 2 Up                667 0.668

# Confusion matrix for train dataset
demo_tib %>% 
  unnest(cols = c(train, train_direction)) %>% 
  count(direction, train_direction) %>% 
  mutate(prop = n / sum(n)) %>% 
  arrange(desc(direction))

## # A tibble: 4 x 4
##   direction train_direction     n  prop
##   <fct>     <chr>           <int> <dbl>
## 1 Up        Down              156 0.156
## 2 Up        Up                351 0.352
## 3 Down      Down              175 0.175
## 4 Down      Up                316 0.317

We could reformat the output into a matrix to make it easier to read.

demo_tib %>% 
  unnest(cols = c(train, train_direction)) %>% 
  count(direction, train_direction) %>% 
  mutate(prop = n / sum(n)) %>% 
  select(-n) %>% 
  pivot_wider(names_from = train_direction, values_from = prop)

## # A tibble: 2 x 3
##   direction  Down    Up
##   <fct>     <dbl> <dbl>
## 1 Down      0.175 0.317
## 2 Up        0.156 0.352

# Model assessment (accuracy/error) for train dataset
demo_tib %>% 
  unnest(cols = c(train, train_direction)) %>% 
  mutate(correct = if_else(train_direction == direction, 1, 0)) %>% 
  summarise(train_accuracy = mean(correct),
            train_error    = 1 - train_accuracy)

## # A tibble: 1 x 2
##   train_accuracy train_error
##            <dbl>       <dbl>
## 1          0.527       0.473

# Model predictions for test dataset
demo_tib <- demo_tib %>%
  mutate(test_prob = map2(mod_01, test, predict, type = "response"),
         test_direction = map(test_prob, ~ if_else(.x > 0.5, "Up", "Down")))

# Model assessment (accuracy/error) for test dataset
demo_tib %>% 
  unnest(cols = c(test, test_direction)) %>% 
  mutate(correct = if_else(test_direction == direction, 1, 0)) %>% 
  summarise(test_accuracy = mean(correct),
            test_error    = 1 - test_accuracy)

## # A tibble: 1 x 2
##   test_accuracy test_error
##           <dbl>      <dbl>
## 1         0.480      0.520

# Confusion matrix for test dataset
demo_tib %>% 
  unnest(cols = c(test, test_direction)) %>% 
  mutate(correct = if_else(test_direction == direction, 1, 0)) %>% 
  count(test_direction, direction) %>% 
  mutate(prop = n / sum(n))

## # A tibble: 4 x 4
##   test_direction direction     n  prop
##   <chr>          <fct>     <int> <dbl>
## 1 Down           Down         77 0.306
## 2 Down           Up           97 0.385
## 3 Up             Down         34 0.135
## 4 Up             Up           44 0.175

# reformated confusion matrix for presentation
demo_tib %>% 
  unnest(cols = c(test, test_direction)) %>% 
  mutate(correct = if_else(test_direction == direction, 1, 0)) %>% 
  count(test_direction, direction) %>% 
  mutate(prop = n / sum(n)) %>% 
  select(-n) %>% 
  pivot_wider(names_from = test_direction, values_from = prop)

## # A tibble: 2 x 3
##   direction  Down    Up
##   <fct>     <dbl> <dbl>
## 1 Down      0.306 0.135
## 2 Up        0.385 0.175

Time to add some other models.

glm_fits <- data_db %>% 
  mutate(mod_01 = map(train, glm, 
                      formula = direction ~ lag1 + lag2 + lag3 + lag4 + lag5 + volume,
                      family = binomial),
         mod_02 = map(train, glm, 
                      formula = direction ~ lag1 + lag2,
                      family = binomial),
         mod_03 = map(train, glm, 
                      formula = direction ~ lag1*lag2,
                      family = binomial),
         mod_04 = map(train, glm, 
                      formula = direction ~ lag1 + volume,
                      family = binomial),
         mod_05 = map(train, glm, 
                      formula = direction ~ lag1*volume,
                      family = binomial)) %>% 
  pivot_longer(cols = contains("mod_"), names_to = "model_name", values_to =  "model_fit")

4.2.0.1 Helper functions

The following are user defined functions calculate error rates and confusion matric for glm fits.

# Function to calculate error rate
error_rate_glm <- function(data, model){
  data %>% 
    mutate(pred_prob = predict(model, newdata = data, type = "response"),
           pred_direction = if_else(pred_prob > 0.5, "Up", "Down"),
           error = pred_direction != direction) %>% 
    pull(error) %>% 
    mean()
}

# Function to form confusion matrix
confusion_mat_glm <- function(data, model){
  data %>% 
    mutate(pred_prob = predict(model, newdata = data, type = "response"),
           pred_direction = if_else(pred_prob > 0.5, "Up", "Down")) %>% 
    count(direction, pred_direction) %>% 
    mutate(prop = n / sum(n))
}

Make use of the user defined functions on our glm fits.

# Calculate model error
glm_fits <- glm_fits %>% 
  mutate(train_error = map2_dbl(train, model_fit, error_rate_glm),
         test_error  = map2_dbl(test, model_fit, error_rate_glm),
         test_confusion = map2(test, model_fit, confusion_mat_glm))  
  
glm_fits %>% 
  select(model_name, train_error, test_error) %>% 
  # select_if(~ !is_list(.)) %>% 
  arrange(test_error) %>% 
  kable()

model_name	train_error	test_error
mod_02	0.4839679	0.4404762
mod_03	0.4829659	0.4404762
mod_04	0.4709419	0.4841270
mod_05	0.4619238	0.5039683
mod_01	0.4729459	0.5198413

# contains all info associated with mod_02
glm_fits %>% 
  filter(model_name == "mod_02") %>% 
  unnest(test_confusion)

## # A tibble: 4 x 10
##   train test  model_name model_fit train_error test_error direction
##   <lis> <lis> <chr>      <list>          <dbl>      <dbl> <fct>    
## 1 <tib… <tib… mod_02     <glm>           0.484      0.440 Down     
## 2 <tib… <tib… mod_02     <glm>           0.484      0.440 Down     
## 3 <tib… <tib… mod_02     <glm>           0.484      0.440 Up       
## 4 <tib… <tib… mod_02     <glm>           0.484      0.440 Up       
## # … with 3 more variables: pred_direction <chr>, n <int>, prop <dbl>

# show only confusion matrix info for mod_02 -- clean up output
glm_fits %>% 
  filter(model_name == "mod_02") %>% 
  unnest(test_confusion) %>% 
  select_if(~ !is.list(.))

## # A tibble: 4 x 7
##   model_name train_error test_error direction pred_direction     n  prop
##   <chr>            <dbl>      <dbl> <fct>     <chr>          <int> <dbl>
## 1 mod_02           0.484      0.440 Down      Down              35 0.139
## 2 mod_02           0.484      0.440 Down      Up                76 0.302
## 3 mod_02           0.484      0.440 Up        Down              35 0.139
## 4 mod_02           0.484      0.440 Up        Up               106 0.421

4.3 Linear Discriminant Analysis

# Fit lda models
lda_fits <- data_db %>% 
  mutate(mod_01 = map(train, ~ lda(formula = direction ~ lag1 + lag2 + lag3 + lag4 + lag5 + volume,
                                   data = .x)),
         mod_02 = map(train, ~ lda(formula = direction ~ lag1 + lag2,
                                   data = .x)),
         mod_03 = map(train, ~ lda(formula = direction ~ lag1*lag2,
                                   data = .x)),
         mod_04 = map(train, ~ lda(formula = direction ~ lag1 + volume,
                                   data = .x)),
         mod_05 = map(train, ~ lda(formula = direction ~ lag1*volume,
                                   data = .x))) %>% 
  pivot_longer(cols = contains("mod_"), names_to = "model_name", values_to = "model_fit")

Useful functions for assessing lda fits.

# Function to calculate lda error rate 
error_rate_lda <- function(data, model){
  data %>% 
    mutate(pred_direction = predict(model, newdata = data) %>% 
             pluck("class"),
           error = pred_direction != direction) %>% 
    pull(error) %>% 
    mean()
}

# Function to form lda confusion matrix
confusion_mat_lda <- function(data, model){
  data %>% 
    mutate(pred_direction = predict(model, newdata = data) %>% 
             pluck("class")) %>% 
    count(direction, pred_direction) %>% 
    mutate(prop = n / sum(n))
}

Apply lda helper functions to the model fits.

# update lda_fits with error and confusion info
lda_fits <- lda_fits %>% 
  mutate(train_error = map2_dbl(train, model_fit, error_rate_lda),
         test_error  = map2_dbl(test, model_fit, error_rate_lda),
         test_confusion = map2(test, model_fit, confusion_mat_lda))  
  
# Compare models by test_error
lda_fits %>% 
  select(model_name, train_error, test_error) %>% 
  arrange(test_error) %>% 
  kable()

model_name	train_error	test_error
mod_02	0.4839679	0.4404762
mod_03	0.4839679	0.4404762
mod_04	0.4709419	0.4841270
mod_05	0.4619238	0.5079365
mod_01	0.4719439	0.5198413

# Get confusion matrix for best model
lda_fits %>% 
  filter(model_name == "mod_02") %>% 
  unnest(test_confusion)

## # A tibble: 4 x 10
##   train test  model_name model_fit train_error test_error direction
##   <lis> <lis> <chr>      <list>          <dbl>      <dbl> <fct>    
## 1 <tib… <tib… mod_02     <lda>           0.484      0.440 Down     
## 2 <tib… <tib… mod_02     <lda>           0.484      0.440 Down     
## 3 <tib… <tib… mod_02     <lda>           0.484      0.440 Up       
## 4 <tib… <tib… mod_02     <lda>           0.484      0.440 Up       
## # … with 3 more variables: pred_direction <fct>, n <int>, prop <dbl>

# show only confusion matrix info best model -- clean up output
lda_fits %>% 
  filter(model_name == "mod_02") %>% 
  unnest(test_confusion) %>% 
  select_if(~ !is.list(.))

## # A tibble: 4 x 7
##   model_name train_error test_error direction pred_direction     n  prop
##   <chr>            <dbl>      <dbl> <fct>     <fct>          <int> <dbl>
## 1 mod_02           0.484      0.440 Down      Down              35 0.139
## 2 mod_02           0.484      0.440 Down      Up                76 0.302
## 3 mod_02           0.484      0.440 Up        Down              35 0.139
## 4 mod_02           0.484      0.440 Up        Up               106 0.421

4.4 Quadratic Discriminant Analysis

# Fit qda models
qda_fits <- data_db %>% 
  mutate(mod_01 = map(train, ~ qda(formula = direction ~ lag1 + lag2 + lag3 + lag4 + lag5 + volume,
                                   data = .x)),
         mod_02 = map(train, ~ qda(formula = direction ~ lag1 + lag2,
                                   data = .x)),
         mod_03 = map(train, ~ qda(formula = direction ~ lag1*lag2,
                                   data = .x)),
         mod_04 = map(train, ~ qda(formula = direction ~ lag1 + volume,
                                   data = .x)),
         mod_05 = map(train, ~ qda(formula = direction ~ lag1*volume,
                                   data = .x))) %>% 
  pivot_longer(cols =  contains("mod_"), names_to = "model_name", values_to = "model_fit")

Useful helper functions to calculate error rate and confusion matrix for qda fits.

# Function to calculate qda error rate 
error_rate_qda <- function(data, model){
  data %>% 
    mutate(pred_direction = predict(model, newdata = data) %>% 
             pluck("class"),
           error = pred_direction != direction) %>% 
    pull(error) %>% 
    mean()
}

# Function to form qda confusion matrix
confusion_mat_qda <- function(data, model){
  data %>% 
    mutate(pred_direction = predict(model, newdata = data) %>% 
             pluck("class")) %>% 
    count(direction, pred_direction, .drop = FALSE) %>% 
    mutate(prop = n / sum(n))
}

Make use of the helper functions.

# update qda_fits with error and confusion info
qda_fits <- qda_fits %>% 
  mutate(train_error = map2_dbl(train, model_fit, error_rate_qda),
         test_error  = map2_dbl(test, model_fit, error_rate_qda),
         test_confusion = map2(test, model_fit, confusion_mat_qda))  
  
# Compare models by test_error
qda_fits %>% 
  select(model_name, train_error, test_error) %>% 
  arrange(test_error) %>% 
  kable()

model_name	train_error	test_error
mod_02	0.4859719	0.4007937
mod_03	0.4669339	0.4603175
mod_05	0.4969940	0.4722222
mod_04	0.5040080	0.5436508
mod_01	0.4579158	0.5555556

# Get confusion matrix for best model
qda_fits %>% 
  filter(model_name == "mod_02") %>% 
  unnest(test_confusion)

## # A tibble: 4 x 10
##   train test  model_name model_fit train_error test_error direction
##   <lis> <lis> <chr>      <list>          <dbl>      <dbl> <fct>    
## 1 <tib… <tib… mod_02     <qda>           0.486      0.401 Down     
## 2 <tib… <tib… mod_02     <qda>           0.486      0.401 Down     
## 3 <tib… <tib… mod_02     <qda>           0.486      0.401 Up       
## 4 <tib… <tib… mod_02     <qda>           0.486      0.401 Up       
## # … with 3 more variables: pred_direction <fct>, n <int>, prop <dbl>

# show only confusion matrix info best model -- clean up output
qda_fits %>% 
  filter(model_name == "mod_02") %>% 
  unnest(test_confusion) %>% 
  select_if(~ !is.list(.))

## # A tibble: 4 x 7
##   model_name train_error test_error direction pred_direction     n   prop
##   <chr>            <dbl>      <dbl> <fct>     <fct>          <int>  <dbl>
## 1 mod_02           0.486      0.401 Down      Down              30 0.119 
## 2 mod_02           0.486      0.401 Down      Up                81 0.321 
## 3 mod_02           0.486      0.401 Up        Down              20 0.0794
## 4 mod_02           0.486      0.401 Up        Up               121 0.480

4.5 K-Nearest Neighbors

#### Helper Functions

# tidy wrapper function for knn
knn_tidy <- function(train, test, pred_vars, response_var, ...){
  train_reduced <- train %>% select(!!pred_vars) %>% as.matrix()
  test_reduced  <- test %>% select(!!pred_vars) %>% as.matrix()
  train_class   <- train %>% select(!!response_var) %>% as.matrix()
 
  preds <- class::knn(train = train_reduced, 
                      test = test_reduced, 
                      cl = train_class, ...) 
  
  pred_name <- paste0("pred_", response_var)
  tibble(!!pred_name := preds)
}

# Function to calculate knn error rate 
error_rate_knn <- function(data, pred_value){
  data %>%
    bind_cols(pred_value) %>% 
    mutate(error = direction != pred_direction) %>% 
    pull(error) %>% 
    mean()
}

# Function to form knn confusion matrix
confusion_mat_knn <- function(data, pred_value){
  data %>%
    bind_cols(pred_value) %>% 
    count(direction, pred_direction) %>% 
    mutate(prop = n / sum(n))
}

# Set-up tibble with predictor vars
pred_var <- tibble(pred_set = list(c("lag1", "lag2", "lag3", 
                                     "lag4", "lag5", "volume"), 
                                   c("lag1", "lag2")))

# Set-up tibble with num of neighbors (k)
k_values <- tibble(k_value = c(1, 5, 10, 15, 20, 40))

# Set-up tibble with model fitting info & fit to test dataset
knn_fits <- data_db %>% 
  crossing(k_values) %>% 
  crossing(pred_var) %>% 
  mutate(knn_preds = pmap(list(train, test, pred_set,"direction", k_value),
                          knn_tidy))

# update knn_fits with error and confusion info
knn_fits <- knn_fits %>% 
  mutate(test_error = map2_dbl(test, knn_preds, error_rate_knn),
         test_confusion = map2(test, knn_preds, confusion_mat_knn)) 
  
# Compare models by test_error
knn_fits %>% 
  select(pred_set, k_value, test_error) %>% 
  mutate(pred_set = map_chr(pred_set, ~ str_c(.x, collapse = ", " ))) %>% 
  arrange(test_error) %>% 
  kable()

pred_set	k_value	test_error
lag1, lag2, lag3, lag4, lag5, volume	1	0.4880952
lag1, lag2, lag3, lag4, lag5, volume	20	0.4880952
lag1, lag2	20	0.4880952
lag1, lag2, lag3, lag4, lag5, volume	40	0.4880952
lag1, lag2	1	0.5000000
lag1, lag2, lag3, lag4, lag5, volume	5	0.5000000
lag1, lag2	10	0.5079365
lag1, lag2, lag3, lag4, lag5, volume	10	0.5119048
lag1, lag2, lag3, lag4, lag5, volume	15	0.5119048
lag1, lag2	40	0.5119048
lag1, lag2	5	0.5158730
lag1, lag2	15	0.5158730

# Get confusion matrix for best model
knn_fits %>% 
  arrange(test_error) %>% 
  pluck("test_confusion", 1)

## # A tibble: 4 x 4
##   direction pred_direction     n  prop
##   <fct>     <fct>          <int> <dbl>
## 1 Down      Down              50 0.198
## 2 Down      Up                61 0.242
## 3 Up        Down              62 0.246
## 4 Up        Up                79 0.313